Los ordenadores al escribir no reciben la información que realmente pulsamos en las teclas del teclado si no que utiliza un código diferente llamado el sistema de numeración binario está basado en unos (1) y ceros (0) , las corrientes altas son los unos y las corrientes bajas los ceros.

2 Define sistema de numeración decimal y binario.
El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras : cero (0) - uno (1) - dos (2) - tres (3) - cuatro (4) - cinco (5) - seis (6) - siete (7) - ocho (8) y nueve (9).
El sistema binario, llamado también sistema diádico 1 en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los sistemas que se utilizan en los ordenadores, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
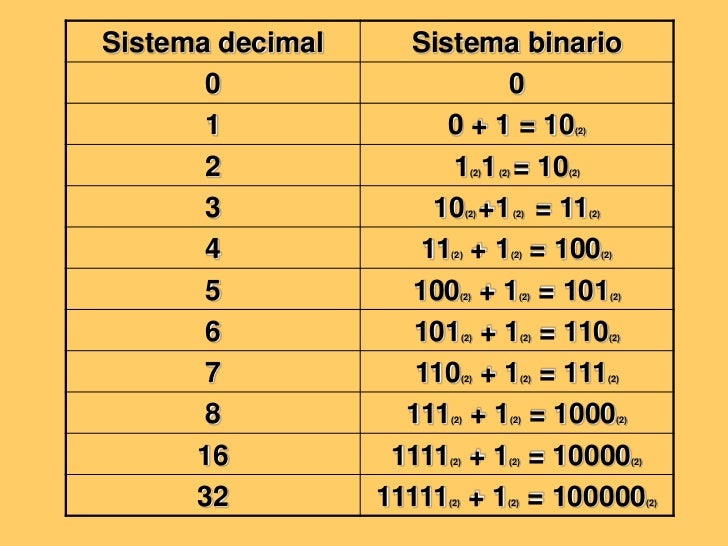
3 Explica cómo se pasa de sistema binario a decimal y viceversa. (Ejemplos)
Pasar de un número binario en su equivalente decimal:
En sistema decimal, las cifras que componen un número son las cantidades que están multiplicando a las distintas potencias de diez (10, 100, 1000, 10000, etc.)
Por ejemplo, 745 = 7 · 100 + 4 · 10 + 5 · 1
O lo que es lo mismo: 745 = 7 · 102 + 4 · 101 + 5 · 100
En el sistema binario, las cifras que componen el número multiplican a las potencias de dos (1, 2, 4, 8, 16, ….)
20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, ...
Por ejemplo, para pasar a binario un número decimal, empezamos por la derecha y vamos multiplicando cada cifra por las sucesivas potencias de 2, avanzando hacia la izquierda:
101102 = 0 · 1 + 1 · 2 + 1 · 4 + 0 · 8 + 1 · 16 = 2 + 4 + 16 = 2210
1102 = 0 · 1 + 1 · 2 + 1 · 4 = 2 + 4 = 610
Pasar de un número decimal en su equivalente binario
Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).
La lista de ceros y unos leídos de abajo a arriba es el resultado.
Procedimiento:
- Dividir entre 2 sucesivamente
- Apuntar el resultado y el resto de cada operación
- Apuntar a lista de ceros y unos de abajo a arriba
Actividades de la página 74 ( 3,4 y 5)
3 ¿De cuántos dígitos se dispone, en el sistema de numeración decimal, para representar un número cualquiera? ¿Y en el sistema de numeración binario?
En el sistema de numeración decimal se dispone de 10 dígitos (0,1,2,3,4,5,6,7,8,9).
En el sistema de numeración binario se dispone de 2 dígitos ( 0,1).
4 Convierte el número binario 1110011 en su equivalente decimal.
1110011= 64+ 32+ 16+ 2+ 1= 115
5 ¿Cuál es el número binario equivalente al decimal 67?
67= 64 + 2+ 1= 1000011
No hay comentarios:
Publicar un comentario